今週ツイッターユーザーの皆様へ出した挑戦状「Twitter Challenge」に多くの方が挑戦してくださったようで、ありがとうございました!
解答は木曜いっぱいまでで締め切らせて頂きました。
今回の問題は「中学生レベル」という触れ込みで出したのですが、
解いてくれたのは高校生が一番多かったです。
やはり
中学生レベルの問題を高校生が解けないんじゃ話にならない
という気持ちが働いたのかもしれません。
が、所詮ただのお遊び。
正解できなくても何ら気にする必要はありません。

(πのパイ)
正解者発表
今回、DMで解答を送ってくれたのは10人。
そして正解者は3人のみでした。
結構難しかったかもしれませんね。
ということで、今回正解したのは、
正解者① ふりっぱさん(@flippa4869)
正解者② とむっきぃさん(@tomkky423)
正解者③ フレイちゃんさん(@fley_01)
以上の3名です!
おめでとうございます!!
「問題難しすぎありえない。dai死ね」
こんな声も聞こえたり聞こえなかったりしましたが、
3人はきっちり答えを出してくれました。
事前にヒントとして「相似と面積比使えばいいよー」と呟いていたのですが、
ふりっぱさんなんかはそれとは別の考え方で、関数を使ってグラフ化させて答えを出していました。
若い頭の発想は凄いですね。
問題の正解
それでは今回の問題の正解を発表します。
解法
図のように補助線を引きます。
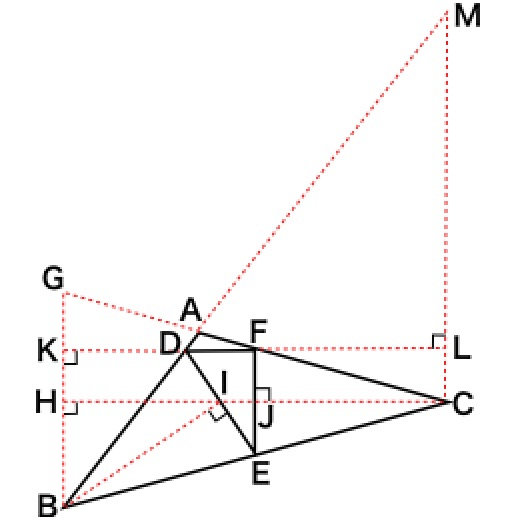
(問題より、条件として∠DFE=90°、DF=4cm、FE=6cm、
DB=BE=EC=CFが与えられています。)
△EJIと△EFDは相似であり、EJ=JFとなるので相似比は1:2です。
つまり、IJ=4÷2=2cmとなります。
続いて、△CFEとCGBも相似になり、BE=ECから相似比は1:2です。
なのでGB=6×2=12cm、HBはその半分で6cmです。
さらに、△DEFと△BIHも相似です。(2つの角度が等しい)
HB:FD=6:4=3:2から、相似比は3:2です。
なのでHIは6÷2/3=9cmですね。
これらを踏まえると、
HJ=9+2=11cm、HCはその2倍だから22cm、
△CGBの面積は12×22÷2=132cm2となります。
後は、GA:ACの比率がわかれば、
△CGBとの面積比で△ABCの面積が出せます。
△KBDと△LMDは相似であり、
KD=11-4=7cm、DL=22-7=15cmから、相似比は7:15です。
KB=KH+HB=FJ+HB=3+6=9なので、
LM=9÷7/15=135/7となります。
次に、LC=FJ=3cmから、CM=3+135/7=156/7ですね。
△GBAと△CMAは相似であり、
相似比はGB:CM=12:(156/7)=7:13。
よってGA:AC=7:13。
したがって、△ABCの面積は△CGBの13/20なので、
△ABC=132×13/20=429/5となります。
答え:429/5cm2 (または85.8cm2)
いかがでしたか?
中学生レベルとはいえここまで補助線を引かせるのは想定外だったかもしれません。
が、値が不十分な条件で面積を出せという問題が出たら、
このように補助線を引いて相似からの面積比で求めるのは1つのセオリーでもあります。
もし今後似たような問題が学校のテストなどで出たら、役立ててもらえたらと思います。
次回予告
次回のTwitter Challengeは具体的な日時はまだわかりませんが、
近日中に出題したいと思います。
次回のテーマは「謎解き」です。
数学が苦手だから今回はパスしたという方も、
次回は頭のひらめきをフルに使って参加してもらえたらと思います。
今後のTwitter Challengeもよろしくお願いします!
ではでは!


